Deben traer la consulta de qué es álgebra?
Raíces o breve historia del álgebra.
ÁLGEBRA
La palabra álgebra proviene del vocablo Árabe "al jarb" que significa ciencia de la transposición y la reducción., del paso y el arreglo, del intercambio y el manejo. Se emplea para sintetizar los diferentes conceptos de ciencias como la física, química, geometría analítica y cálculo. Proporciona también una serie de instrucciones útiles par obtener resultados en el menor tiempo posible, de una forma ordenada y práctica, utilizando un código combinado de letras, números y signos de relación y operación.
El álgebra es uno de varios sistemas simbólicos empleados para manejas transformaciones sobre los números enteros y fraccionarios.
Notación algebraica
Consiste en que los números se emplean para representar cantidades conocidas y determinadas. Las letras se emplean para representar toda clase de cantidades, ya sean conocidas o desconocidas. Las cantidades conocidas se expresan por las primeras letras del alfabeto: a, b, c, d, … Las cantidades desconocidas se representan por las últimas letras del alfabeto: u, v, w, x, y, z.13
Los signos empleados en álgebra son tres clases: Signos de operación, signos de relación y signos de agrupación.13
Signos de operación
En álgebra se verifican con las cantidades las mismas operaciones que en aritmética: suma, resta,multiplicación, elevación a potencias y extracción de raíces, que se indican con los principales signos de aritmética excepto el signo de multiplicación. En lugar del signo × suele emplearse un punto entre los factores y también se indica a la multiplicación colocando los factores entre paréntesis. Así a⋅b y (a)(b) equivale a a × b.
Signos de relación
Se emplean estos signos para indicar la relación que existe entre dos cantidades. Los principales son: =, que se lee igual a. Así, a=b se lee “a igual a b”. >, que se lee mayor que. Así, x + y > m se lee “x + y mayor que m”. <, que se lee menor que. Así, a < b + c se lee “amenor que b + c”.
Signos de agrupación
Los signos de agrupación son: el paréntesis ordinario ( ), el paréntesis angular o corchete [ ], las llaves { } y la barra o vínculo ||. Estos signos indican que la operación colocada entre ellos debe efectuarse primero. Así, (a + b)c índica que el resultado de la suma a y b debe multiplicarse por c; [a – b]m indica que la diferencia entre a y b debe multiplicarse por m, {a + b} ÷ {c – d} índica que la suma de a y bdebe dividirse entre la diferencia de c y d. El orden de estos signos son de la siguiente forma { [ ( ) ] }, por ejemplo: { [ (a + b) - c] ⋅ d} indica que al resultado de la suma de a + b debe restarse c y el resultado de esto multiplicarse por d.
Signos y símbolos más comunes
Los signos y símbolos son utilizados en el álgebra — y en general en teoría de conjuntos y álgebra de conjuntos — con los que se constituyen ecuaciones, matrices, series, etc. Sus letras son llamadas variables, ya que se usa esa misma letra en otros problemas y su valor va variando.
Aquí algunos ejemplos:
| Signos y símbolos | |
| + | Además de expresar adición también es usada para expresar operaciones binarias |
| c o k | Expresan términos constantes |
| Primeras letras del abecedario a, b, c,... | Se utilizan para expresar cantidades conocidas |
| Últimas letras del abecedario ..., x, y, z | Se utilizan para expresar incógnitas |
| n | Expresa cualquier número (1,2,3,4,...,n) |
Exponentes y subindices | Expresar cantidades de la misma especie, de diferente magnitud. |
| Simbología de Conjuntos14 | |
| {} | conjunto |
| ∈ | Es un elemento del conjunto o pertenece al conjunto. |
| ∉ | No es un elemento del conjunto o no pertenece al conjunto. |
| ⎜ | Tal que. |
| n (C) | Cardinalidad del conjunto C. |
| U | Conjunto Universo. |
| Φ | Conjunto Vacío. |
| ⊆ | Subconjunto de. |
| ⊂ | Subconjunto propio de. |
| ⊄ | No es subconjunto propio de. |
| > | Mayor que. |
| < | Menor que. |
| ≥ | Mayor o igual que. |
| ≤ | Menor o igual que. |
| ∩ | Intersección de conjuntos. |
| ∪ | Unión de Conjuntos. |
| A' | Complemento del conjunto A. |
| = | Símbolo de igualdad. |
| ≠ | No es igual a. |
| ... | El conjunto continúa. |
| ⇔ | Si y sólo si. |
| ¬ (en algunos ocasiones ∼) | No, negación lógica (es falso que). |
| ∧ | Y |
| ∨ | O |
Lenguaje algebraico14
Lenguaje común
Lenguaje algebraico
Un número cualquiera. m Un número cualquiera aumentado en siete. m + 7 La diferencia de dos números cualesquiera. f - q El doble de un número excedido en cinco. 2x + 5 La división de un número entero entre su antecesor x/(x-1) La mitad de un número. d/2 El cuadrado de un número y^2 La semisuma de dos números (b+c)/2 Las dos terceras partes de un número disminuidos en cinco es igual a 12. 2/3 (x-5) = 12 Tres números naturales consecutivos. x, x + 1, x + 2. La parte mayor de 1200, si la menor es w 1200 - w El cuadrado de un número aumentado en siete. b2 + 7 Las tres quintas partes de un número más la mitad de su consecutivo equivalen a tres. 3/5 p + 1/2 (p+1) = 3 El producto de un número con su antecesor equivalen a 30. x(x-1) = 30 El cubo de un número más el triple del cuadrado de dicho número. x3 + 3x2
Lenguaje algebraico
¿A qué llamamos Términos?; Expresiones Algebraicas
Se llama: Término.
Un Término separamos de otro, con los signos más o menos:
Un Término separamos de otro, con los signos más o menos:
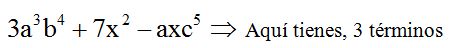
Un Término consta de dos partes: numérica y literal.
Numérica: Es el número que va delante de las letras – también se le llama coeficiente - (si no lleva ninguna cifra, recuerda que lleva el 1).
Literal: Es la compuesta por letras con sus exponentes, si los tienen.
Literal: Es la compuesta por letras con sus exponentes, si los tienen.
Expresión algebraica:
Se llama a un conjunto de letras y números ligados por los signos de las operaciones aritméticas.
Monomio: Se llama monomio a la expresión algebraica que tiene un solo término.
Ejemplos de expresiones algebraicas de un solo término:
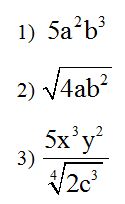
Binomio: Se llama binomio a la expresión algebraica que tiene dos términos.
Ejemplos de expresiones algebraicas de dos términos:
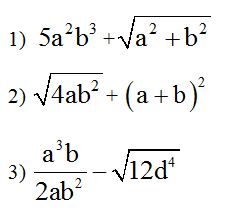
Trinomio: Se llama trinomio a la expresión algebraica que tiene tres términos.
Ejemplo:
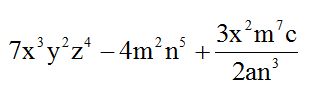
Las expresiones algebraicas que contienen más de tres términos se llaman Polinomios.
9.3 Escribe en lenguaje algebraico:
Tres veces un número es mayor que si al número le sumamos 12.
Respuesta: 3a > a + 12
9.4 La expresión: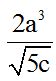 
¿es un monomio o un binomio?
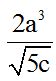¿es un monomio o un binomio?
Respuesta: Es un monomio, tiene un solo término aunque éste sea un cociente indicado
![\frac{\sqrt[3]{7}+1}{2}=1\text{,}456465591386194\ldots](http://upload.wikimedia.org/math/f/9/e/f9e0469fdfd9e2047c07e37776ca52da.png)
es irracional y su expansión decimal es aperiódica.
.
