SEPTIEMBRE 28 AL 2 DE OCTUBRE
TALLERES DE PRODUCTOS Y COCIENTES NOTABLES.
EVALUACIONES DE NIVELACIÓN DEL TERCER PERÍODO.
EVALUACIÓN DE COCIENTES Y PRODUCTOS NOTABLES.
TALLER LUNES 28 ---- 8º A
domingo, 27 de septiembre de 2015
domingo, 20 de septiembre de 2015
SEMANA 33
SEPTIEMBRE 21 AL 25
COCIENTES NOTABLES.
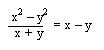
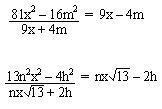
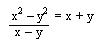
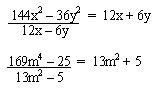 2. CUBOS:
2. CUBOS:
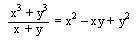

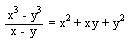

COCIENTES NOTABLES.
COCIENTES NOTABLES
Los cocientes notables resultan de
divisiones exactas entre polinomios que presentan regularidades y permiten
obtener EL RESULTADO SIN EFECTUAR LA DIVISION
INDICADA.
1. CUADRADOS:
A. Cociente de la diferencia de el cuadrado de dos cantidades entre la suma de estas cantidades.
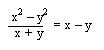
El cociente de la diferencia del cuadrado de dos cantidades entre la suma de estas cantidades es igual a la diferencia de estas cantidades.
Ejemplos:
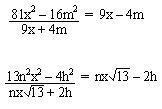
B. Cociente de la diferencia de el cuadrado de dos cantidades entre la diferencia de estas cantidades.
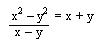
El cociente de la diferencia del cuadrado de dos cantidades entre
la diferencia de estas cantidades es igual a la suma de estas cantidades.
la diferencia de estas cantidades es igual a la suma de estas cantidades.
Ejemplos:
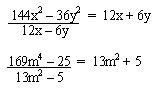
A. Cociente de la suma de el cubo de dos cantidades entre la suma de estas cantidades.
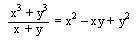
El cociente de la suma del cubo de dos cantidades dividida entre la suma de estas cantidades es igual al cuadrado de la primera menos el producto de estas, más el cuadrado de la segunda( DE LOS DENOMINADORES).
Ejemplos:

B. Cociente de la diferencia de el cubo de dos cantidades entre la diferencia de estas cantidades.
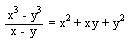
El cociente de la diferencia del cubo de dos cantidades dividida
entre la diferencia de estas cantidades es igual al cuadrado de la
primera más el producto de estas, más el cuadrado de la segunda ( DE LOS DENOMINADORES).
entre la diferencia de estas cantidades es igual al cuadrado de la
primera más el producto de estas, más el cuadrado de la segunda ( DE LOS DENOMINADORES).
Ejemplos:

miércoles, 16 de septiembre de 2015
domingo, 13 de septiembre de 2015
SEMANA 32
SEPTIEMBRE 14 AL 18
BINOMIO DE NEWTON Y TALLER APLICATIVO AL BINOMIO.
La fórmula que nos permite hallar las potencias de un binomio se conoce como binomio de Newton.
Podemos observar que:
El número de términos es n+1.
Los coeficientes son números combinatorios que corresponden a la fila enésima del triángulo de Tartaglia.

En el desarrollo del binomio los exponentes de a van disminuyendo, de uno en uno, de n a cero; y los exponentes de b van aumentando, de uno en uno, de cero a n, de tal manera que la suma de los exponentes de a y de b en cada término es igual a n.
En el caso que uno de los términos del binomio sea negativo, se alternan los signos positivos y negativos.
Ejercicios del binomio de Newton
1. 



2.



domingo, 6 de septiembre de 2015
SEMANA 31
SEPTIEMBRE 7 A 11
TALLER APLICANDO EL TRIÁNGULO DE PASCAL
TALLER APLICANDO TODOS LOS CASOS DE PRODUCTOS NOTABLES.
TALLER APLICANDO EL TRIÁNGULO DE PASCAL
TALLER APLICANDO TODOS LOS CASOS DE PRODUCTOS NOTABLES.
Suscribirse a:
Comentarios (Atom)

