JUNIO 29 A JULIO 3
JUNIO 29----FESTIVO
JUNIO 30---8A
JULIO 1----8B
1. REPASO DE EXPRESIONES ALGEBRAICAS Y CLASIFICACIÓN DE LAS MISMAS, TÉRMINO ALGEBRAICO,ELEMENTOS QUE CONFORMAN UN TÉRMINO ALGEBRAICO GRADO ABSOLUTO Y RELATIVO DE UN TÉRMINO ALGEBRAICO.
2. GRADO ABSOLUTO Y GRADO RELATIVO DE UN POLINOMIO.
3. ORDEN ASCENDENTE Y DESCENDENTE DE UN POLINOMIO.
4. CLASIFICACIÓN DE LOS TÉRMINOS ALGEBRAICOS
5. TALLER Nº 1 DE LOS TEMAS ANTERIORES.
6. SE ANUNCIA EVALUACIÓN PARA PRÓXIMO LUNES 6 DE JULIO.
domingo, 5 de julio de 2015
domingo, 7 de junio de 2015
domingo, 31 de mayo de 2015
SEMANA 20
JUNIO 1 AL 5
Deben traer la consulta de qué es álgebra?
Raíces o breve historia del álgebra.
ÁLGEBRA
La palabra álgebra proviene del vocablo Árabe "al jarb" que significa ciencia de la transposición y la reducción., del paso y el arreglo, del intercambio y el manejo. Se emplea para sintetizar los diferentes conceptos de ciencias como la física, química, geometría analítica y cálculo. Proporciona también una serie de instrucciones útiles par obtener resultados en el menor tiempo posible, de una forma ordenada y práctica, utilizando un código combinado de letras, números y signos de relación y operación.
El álgebra es uno de varios sistemas simbólicos empleados para manejas transformaciones sobre los números enteros y fraccionarios.

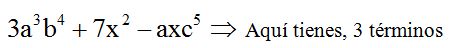
Monomio: Se llama monomio a la expresión algebraica que tiene un solo término.
Ejemplos de expresiones algebraicas de un solo término:
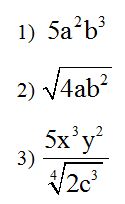
Ejemplos de expresiones algebraicas de dos términos:
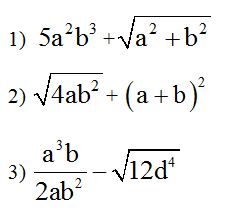
Ejemplo:
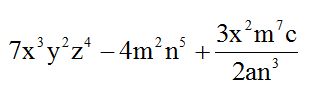
Tres veces un número es mayor que si al número le sumamos 12.
Respuesta: 3a > a + 12
Deben traer la consulta de qué es álgebra?
Raíces o breve historia del álgebra.
ÁLGEBRA
La palabra álgebra proviene del vocablo Árabe "al jarb" que significa ciencia de la transposición y la reducción., del paso y el arreglo, del intercambio y el manejo. Se emplea para sintetizar los diferentes conceptos de ciencias como la física, química, geometría analítica y cálculo. Proporciona también una serie de instrucciones útiles par obtener resultados en el menor tiempo posible, de una forma ordenada y práctica, utilizando un código combinado de letras, números y signos de relación y operación.
El álgebra es uno de varios sistemas simbólicos empleados para manejas transformaciones sobre los números enteros y fraccionarios.
Notación algebraica
Consiste en que los números se emplean para representar cantidades conocidas y determinadas. Las letras se emplean para representar toda clase de cantidades, ya sean conocidas o desconocidas. Las cantidades conocidas se expresan por las primeras letras del alfabeto: a, b, c, d, … Las cantidades desconocidas se representan por las últimas letras del alfabeto: u, v, w, x, y, z.13
Los signos empleados en álgebra son tres clases: Signos de operación, signos de relación y signos de agrupación.13
Signos de operación
En álgebra se verifican con las cantidades las mismas operaciones que en aritmética: suma, resta,multiplicación, elevación a potencias y extracción de raíces, que se indican con los principales signos de aritmética excepto el signo de multiplicación. En lugar del signo × suele emplearse un punto entre los factores y también se indica a la multiplicación colocando los factores entre paréntesis. Así a⋅b y (a)(b) equivale a a × b.
Signos de relación
Se emplean estos signos para indicar la relación que existe entre dos cantidades. Los principales son: =, que se lee igual a. Así, a=b se lee “a igual a b”. >, que se lee mayor que. Así, x + y > m se lee “x + y mayor que m”. <, que se lee menor que. Así, a < b + c se lee “amenor que b + c”.
Signos de agrupación
Los signos de agrupación son: el paréntesis ordinario ( ), el paréntesis angular o corchete [ ], las llaves { } y la barra o vínculo ||. Estos signos indican que la operación colocada entre ellos debe efectuarse primero. Así, (a + b)c índica que el resultado de la suma a y b debe multiplicarse por c; [a – b]m indica que la diferencia entre a y b debe multiplicarse por m, {a + b} ÷ {c – d} índica que la suma de a y bdebe dividirse entre la diferencia de c y d. El orden de estos signos son de la siguiente forma { [ ( ) ] }, por ejemplo: { [ (a + b) - c] ⋅ d} indica que al resultado de la suma de a + b debe restarse c y el resultado de esto multiplicarse por d.
Signos y símbolos más comunes
Los signos y símbolos son utilizados en el álgebra — y en general en teoría de conjuntos y álgebra de conjuntos — con los que se constituyen ecuaciones, matrices, series, etc. Sus letras son llamadas variables, ya que se usa esa misma letra en otros problemas y su valor va variando.
Aquí algunos ejemplos:
| Signos y símbolos | |
| + | Además de expresar adición también es usada para expresar operaciones binarias |
| c o k | Expresan términos constantes |
| Primeras letras del abecedario a, b, c,... | Se utilizan para expresar cantidades conocidas |
| Últimas letras del abecedario ..., x, y, z | Se utilizan para expresar incógnitas |
| n | Expresa cualquier número (1,2,3,4,...,n) |
Exponentes y subindices | Expresar cantidades de la misma especie, de diferente magnitud. |
| Simbología de Conjuntos14 | |
| {} | conjunto |
| ∈ | Es un elemento del conjunto o pertenece al conjunto. |
| ∉ | No es un elemento del conjunto o no pertenece al conjunto. |
| ⎜ | Tal que. |
| n (C) | Cardinalidad del conjunto C. |
| U | Conjunto Universo. |
| Φ | Conjunto Vacío. |
| ⊆ | Subconjunto de. |
| ⊂ | Subconjunto propio de. |
| ⊄ | No es subconjunto propio de. |
| > | Mayor que. |
| < | Menor que. |
| ≥ | Mayor o igual que. |
| ≤ | Menor o igual que. |
| ∩ | Intersección de conjuntos. |
| ∪ | Unión de Conjuntos. |
| A' | Complemento del conjunto A. |
| = | Símbolo de igualdad. |
| ≠ | No es igual a. |
| ... | El conjunto continúa. |
| ⇔ | Si y sólo si. |
| ¬ (en algunos ocasiones ∼) | No, negación lógica (es falso que). |
| ∧ | Y |
| ∨ | O |
Lenguaje algebraico14
Lenguaje común
Lenguaje algebraico
Un número cualquiera. m Un número cualquiera aumentado en siete. m + 7 La diferencia de dos números cualesquiera. f - q El doble de un número excedido en cinco. 2x + 5 La división de un número entero entre su antecesor x/(x-1) La mitad de un número. d/2 El cuadrado de un número y^2 La semisuma de dos números (b+c)/2 Las dos terceras partes de un número disminuidos en cinco es igual a 12. 2/3 (x-5) = 12 Tres números naturales consecutivos. x, x + 1, x + 2. La parte mayor de 1200, si la menor es w 1200 - w El cuadrado de un número aumentado en siete. b2 + 7 Las tres quintas partes de un número más la mitad de su consecutivo equivalen a tres. 3/5 p + 1/2 (p+1) = 3 El producto de un número con su antecesor equivalen a 30. x(x-1) = 30 El cubo de un número más el triple del cuadrado de dicho número. x3 + 3x2
Lenguaje algebraico
¿A qué llamamos Términos?; Expresiones Algebraicas

Se llama: Término.
Un Término separamos de otro, con los signos más o menos:
Un Término separamos de otro, con los signos más o menos:
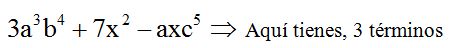
Un Término consta de dos partes: numérica y literal.
Numérica: Es el número que va delante de las letras – también se le llama coeficiente - (si no lleva ninguna cifra, recuerda que lleva el 1).
Literal: Es la compuesta por letras con sus exponentes, si los tienen.
Literal: Es la compuesta por letras con sus exponentes, si los tienen.
Expresión algebraica:
Se llama a un conjunto de letras y números ligados por los signos de las operaciones aritméticas.
Monomio: Se llama monomio a la expresión algebraica que tiene un solo término.
Ejemplos de expresiones algebraicas de un solo término:
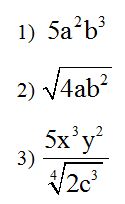
Binomio: Se llama binomio a la expresión algebraica que tiene dos términos.
Ejemplos de expresiones algebraicas de dos términos:
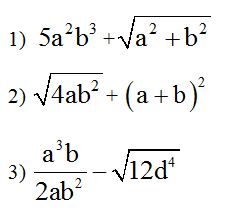
Trinomio: Se llama trinomio a la expresión algebraica que tiene tres términos.
Ejemplo:
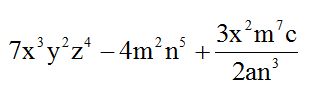
Las expresiones algebraicas que contienen más de tres términos se llaman Polinomios.
9.3 Escribe en lenguaje algebraico:
Tres veces un número es mayor que si al número le sumamos 12.
Respuesta: 3a > a + 12
9.4 La expresión: 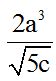 ¿es un monomio o un binomio?
¿es un monomio o un binomio?
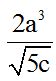 ¿es un monomio o un binomio?
¿es un monomio o un binomio?
Respuesta: Es un monomio, tiene un solo término aunque éste sea un cociente indicado
domingo, 24 de mayo de 2015
SEMANA 19
MAYO 25 AL 29
IMPORTANTE:
En esta semana se realizarán evaluaciones escritas de los diferentes temas trabajados en el período, como:
Números Reales y operaciones con los mismos( suma, resta, multiplicación, división con reales, ecuaciones, potenciación y propiedades de la potenciación, radicación con reales)
Notación científica.
TALLERES TRABAJADOS TAMBIÉN EN EL SEGUNDO PERÍODO ESCOLAR, LOS CUALES TODOS DEBEN TENER SOLUCIONADOS YA QUE SE EVALUARÁ EN CLASE.
CONSULTA: Hacerla en el cuaderno de notas.
1. Para qué se usa la notación científica?
2. Escriba algunos ejemplos reales en los cuales se emplea la notación científica en la actualidad.
3. A qué matemático e debemos la notación científica?
IMPORTANTE:
En esta semana se realizarán evaluaciones escritas de los diferentes temas trabajados en el período, como:
Números Reales y operaciones con los mismos( suma, resta, multiplicación, división con reales, ecuaciones, potenciación y propiedades de la potenciación, radicación con reales)
Notación científica.
TALLERES TRABAJADOS TAMBIÉN EN EL SEGUNDO PERÍODO ESCOLAR, LOS CUALES TODOS DEBEN TENER SOLUCIONADOS YA QUE SE EVALUARÁ EN CLASE.
CONSULTA: Hacerla en el cuaderno de notas.
1. Para qué se usa la notación científica?
2. Escriba algunos ejemplos reales en los cuales se emplea la notación científica en la actualidad.
3. A qué matemático e debemos la notación científica?
SEMANA 18
MAYO 18 AL 22
TALLER A REALIZAR DURANTE LA SEMANA
ECUACIONES
NOTACIÓN CIENTÌFICA:
POTENCIACIÓN Y RADICACIÓN CON REALES.
TALLER A REALIZAR DURANTE LA SEMANA
2. Solucione las siguientes operaciones: operaciones:
ECUACIONES
NOTACIÓN CIENTÌFICA:
POTENCIACIÓN Y RADICACIÓN CON REALES.
domingo, 10 de mayo de 2015
SEMANA 17
MAYO 11 AL 15
En la semana 18 encontrarás videos referentes a ecuaciones, suma, resta, multiplicación, divisiòn, potenciación y radicación de reales. igualmente de notación científica.
NÚMEROS REALES
En la semana 18 encontrarás videos referentes a ecuaciones, suma, resta, multiplicación, divisiòn, potenciación y radicación de reales. igualmente de notación científica.
NÚMEROS REALES
Tipos de números reales
Racionales e irracionales
Un número real puede ser un número racional o un número irracional. Los números racionales son aquellos que pueden expresarse como el cociente de dos números enteros, tal como 3/4, -21/3, 5, 0, 1/2, mientras que los irracionales son todos los demás. Los números racionales también pueden describirse como aquellos cuya representación decimal es eventualmente periódica, mientras que los irracionales tienen una expansión decimal aperiódica:
- Ejemplos
- 1/4 = 0,250000... Es un número racional puesto que es periódico a partir del tercer número decimal.
- 5/7 = 0,7142857142857142857.... Es racional y tiene un período de longitud 6 (repite 714285).
![\frac{\sqrt[3]{7}+1}{2}=1\text{,}456465591386194\ldots](http://upload.wikimedia.org/math/f/9/e/f9e0469fdfd9e2047c07e37776ca52da.png) es irracional y su expansión decimal es aperiódica.
es irracional y su expansión decimal es aperiódica.
El conjunto de los números racionales se designa mediante  .
.
 .
.
Los números reales son los que pueden ser expresados por un número
entero (3, 28, 1568) o decimal (4,28; 289,6; 39985,4671). Esto quiere
decir que abarcan a los números racionales (que pueden representarse
como el cociente de dos enteros con denominador distinto a cero) y
los números irracionales (los que no pueden ser expresados como
lunes, 4 de mayo de 2015
lunes, 20 de abril de 2015
SEMANA 14
ABRIL 20 AL 24
ABRIL 22 INICIA PARO NACIONAL DE EDUCADORES.
NOTACIÓN CIENTÍFICA.
ABRIL 22 INICIA PARO NACIONAL DE EDUCADORES.
NOTACIÓN CIENTÍFICA.
La notación científica es una manera rápida de representar un número utilizando potencias de base diez. Esta notación se utiliza para poder expresar muy fácilmente números muy grandes o muy pequeños.
Los números se escriben como un producto:
siendo:
 un número real mayor o igual que 1 y menor que 10, que recibe el nombre de coeficiente.
un número real mayor o igual que 1 y menor que 10, que recibe el nombre de coeficiente. un número entero, que recibe el nombre de exponente u orden de magnitud.
un número entero, que recibe el nombre de exponente u orden de magnitud.
La notación científica utiliza un sistema llamado coma flotante, o de punto flotante en países de habla inglesa y en algunos hispanohablantes.
Historia
El primer intento de representar números demasiado grandes fue emprendido por el matemático y filósofo griego Arquímedes, descrito en su obra El contador de Arena en el siglo III a. C. Ideó un sistema de representación numérica para estimar cuántos granos de arena existían en el universo. El número estimado por él era de 1063 granos. Nótese la coincidencia del exponente con el número de casilleros del ajedrez sabiendo que para valores positivos, el exponente es n-1 donde n es el número de dígitos, siendo la última casilla la Nº 64 el exponente sería 63 (hay un antiguo cuento del tablero de ajedrez en que al último casillero le corresponde -2 elevado a la 63- granos).
A través de la notación científica fue concebido el modelo de representación de los números reales mediante coma flotante.
Escritura
- 100 = 1
- 101 = 10
- 102 = 100
- 103 = 1 000
- 104 = 10 000
- 105 = 100 000
- 106 = 1 000 000
- 107 = 10 000 000
- 108 = 100 000 000
- 109 = 1 000 000 000
- 1010 = 10 000 000 000
- 1020 = 100 000 000 000 000 000 000
- 1030 = 1 000 000 000 000 000 000 000 000 000 000
10 elevado a una potencia entera negativa –n es igual a 1/10n:
- 10–1 = 1/10 = 0,1
- 10–2 = 1/100 = 0,01
- 10–3 = 1/1 000 = 0,001
- 10–9 = 1/1 000 000 000 = 0,000 000 001
- 10-12 = 1/1 000 000 000 000 = 0,000 000 000 001
- 10-15 = 1/1 000 000 000 000 000 = 0,000 000 000 000 001
- 10-17 = 1/ 1 000 000 000 000 000 00 = 0,000 000 000 000 000 01
Por tanto, un número como: 156 234 000 000 000 000 000 000 000 000 debe ser escrito como 1,56234×1029,
y un número pequeño como 0,000 000 000 000 000 000 000 000 000 000 910 939 kg (masa de un electrón) debe ser escrito como 9,10939×10–31kg.
Operaciones matemáticas con notación científica
Suma y resta
Siempre que las potencias de 10 sean las mismas, se deben sumar los coeficientes, dejando la potencia de 10 con el mismo grado. En caso de que no tengan el mismo exponente, debe convertirse el coeficiente, multiplicándolo o dividiéndolo por 10 tantas veces como se necesite para obtener el mismo exponente.
Ejemplos:
- 2×105 + 3×105 = 5×105
- 3×105 - 0.2×105 = 2.8×105
- 2×104 + 3 ×105 - 6 ×103 = (tomamos el exponente 5 como referencia)
- = 0,2 × 105 + 3 × 105 - 0,06 ×105 = 3,14 ×105
Multiplicación
Para multiplicar cantidades escritas en notación científica se multiplican los coeficientes y se suman los exponentes.
Ejemplo:
- (4×1012)×(2×105) =8×1017
División
Para dividir cantidades escritas en notación científica se dividen los coeficientes y se restan los exponentes.
Ejemplo: 

 .
.


 .
.Potenciación
Se eleva el coeficiente a la potencia y se multiplican los exponentes.
Ejemplo: (3×106)2 = 9 ×1012.
Radicación
Se debe extraer la raíz del coeficiente y se divide el exponente entre el índice de la raíz.
Ejemplos:
domingo, 12 de abril de 2015
SEMANA DOCE
ABRIL 6 AL 10
ABRIL 6---CALAMIDAD DOMÉSTICA---NO DICTÉ CLASES
ABRIL 7 AL 10
Historia de los números irracionales
ABRIL 6---CALAMIDAD DOMÉSTICA---NO DICTÉ CLASES
ABRIL 7 AL 10
Historia de los números irracionales
Aparentemente Hipaso (un estudiante de Pitágoras) descubrió los números irracionales intentando escribir la raíz de 2 en forma de fracción (se cree que usando geometría). Pero en su lugar demostró que no se puede escribir como fracción, así que es irracional.
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!
SEMANA 11
MARZO 23 A 27
MARZO 23-----FESTIVO
CALAMIDAD DOMÉSTICA (NO DICTÉ CLASES TODA LA SEMANA)
MARZO 30 A ABRIL 3----SEMANA SANTA
MARZO 23-----FESTIVO
CALAMIDAD DOMÉSTICA (NO DICTÉ CLASES TODA LA SEMANA)
MARZO 30 A ABRIL 3----SEMANA SANTA
domingo, 15 de marzo de 2015
SEMANA DIEZ
MARZO 16 A 20
IDENTIFICACIÓN DE LOS NÚMEROS IRRACIONALES ( I )
Los números que no se pueden representar por un racional se llaman irracionales. Hay números decimales , cuyas fracciones son periódicas, es decir que se repiten a partir de cierto número. Ejem:
7/3 = 2,333... 32/25= 1,282828... 781/250= 3,124124124...
Son fracciones periódicas y éstas se pueden representar por un racional.
Pero existen otros números cuyos decimales son infinitos, sin repetir períodos y que no pueden escribirse como racionales, esos números son los llamados Irracionales.
Ejm:
Lo mismo ocurre con la raíz cuadrada de dos: 1, 4142136...que se aproxima a 1,4142 aunque no tenga límite.
La raíz de cualquier número natural que no se deja escribir como una potencia. Ejemplos:
a los racionales y "I" los irracionales.
Si unimos los racionales "Q" con los irracionales "I" se forman los reales "R"
Los números irracionales se pueden representar en la RECTA NUMÉRICA.
A cada número racional le corresponde un punto en la recta pero en realidad éstos no completan la recta, también la constituyen los irracionales. En general, representar un número con infinitas cifras decimales no periódicas es imposible y por lo tanto nos tendríamos que conformar con una aproximación. De todas maneras, hay métodos geométricos que permiten representar algunos números irracionales en la recta numérica.
Veamos como se puede representar, por ejemplo, :
hay que tener claro que =1,414...,es decir, 1<
=1,414...,es decir, 1<  < 2
< 2
Observa el cuadrado del dibujo, si ampliamos el teorema de Pitágoras para hallar su diagonal comprendemos esto
Con la ayuda de un compás podemos representar exactamente en la recta numérica.
en la recta numérica.
Sabemos que es un número irracional, por lo tanto,
es un número irracional, por lo tanto,
Historia de los números irracionales
Aparentemente Hipaso (un estudiante de Pitágoras) descubrió los números irracionales intentando escribir la raíz de 2 en forma de fracción (se cree que usando geometría). Pero en su lugar demostró que no se puede escribir como fracción, así que es irracional.
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!
IDENTIFICACIÓN DE LOS NÚMEROS IRRACIONALES ( I )
Los números que no se pueden representar por un racional se llaman irracionales. Hay números decimales , cuyas fracciones son periódicas, es decir que se repiten a partir de cierto número. Ejem:
7/3 = 2,333... 32/25= 1,282828... 781/250= 3,124124124...
Son fracciones periódicas y éstas se pueden representar por un racional.
Pero existen otros números cuyos decimales son infinitos, sin repetir períodos y que no pueden escribirse como racionales, esos números son los llamados Irracionales.
Ejm:
3, 1415275926535897932384626433832795 (y más...) ... que es conocido como pi.
que se aproxima a 3,1416 y que sale de dividir la longitud de la circunferencia entre el diámetro.Lo mismo ocurre con la raíz cuadrada de dos: 1, 4142136...que se aproxima a 1,4142 aunque no tenga límite.
La raíz de cualquier número natural que no se deja escribir como una potencia. Ejemplos:
a los racionales y "I" los irracionales.
Si unimos los racionales "Q" con los irracionales "I" se forman los reales "R"
Los números irracionales se pueden representar en la RECTA NUMÉRICA.
A cada número racional le corresponde un punto en la recta pero en realidad éstos no completan la recta, también la constituyen los irracionales. En general, representar un número con infinitas cifras decimales no periódicas es imposible y por lo tanto nos tendríamos que conformar con una aproximación. De todas maneras, hay métodos geométricos que permiten representar algunos números irracionales en la recta numérica.
Veamos como se puede representar, por ejemplo, :

hay que tener claro que
 =1,414...,es decir, 1<
=1,414...,es decir, 1<  < 2
< 2Observa el cuadrado del dibujo, si ampliamos el teorema de Pitágoras para hallar su diagonal comprendemos esto
Con la ayuda de un compás podemos representar exactamente
 en la recta numérica.
en la recta numérica.Sabemos que
 es un número irracional, por lo tanto,
es un número irracional, por lo tanto,
el punto P de la recta no puede estar ocupado por ningún otro número irracional.
Números irracionales famosos
domingo, 8 de marzo de 2015
SEMANA NUEVE
MARZO 9 AL 13
NÚMEROS IRRACIONALES.
Un número irracional es aquél cuya representación decimal no se puede expresar como el cociente de dos números enteros, es decir como un número racional.
esto significa que un número irracional es una expresión decimal que no es finita y que tampoco es periódica, lo cual implica necesariamente que es un decimal cuyas cifras decimales son infinitas y ninguna porción de estas se repite, es decir, NO TIENE PERÍODO.
Ejemplos:
a) 4, 24681012141618...números pares
b) 1, 3571113171923293137...números primos
c) 1, 12345678910111213...números naturales
NÚMEROS QUE NO SE DEJAN ESCRIBIR COMO POTENCIA
{2,3,5,6,7,10,11,12,13,14,15,17,18,19,20,21,22,23,24,26,28,29,30,31,33,34,35,37,38,39,40,41,42,43,44,45,46,47,48,50,51,53}ñale la parte entera, la parte periódica y la parte no periódica:
TALLER.
SEÑALE LA PARTE ENTERA, LA PARTE PERIÓDICA Y LA PARTE NO PERIÓDICA:
1. 71,403405403403...
2. 102,102102102...
3. 603,989898...
4. 405,505050505...
5. 793,413413413...
6. 49,212121...
7. 503,015989898...
8. 68,213341341341...
9. 500,034415415415...
10. 71,6123939339...
11. 605,101101101...
12. 421,671151515...
Taller de repaso con números racionales.
NÚMEROS IRRACIONALES.
Un número irracional es aquél cuya representación decimal no se puede expresar como el cociente de dos números enteros, es decir como un número racional.
esto significa que un número irracional es una expresión decimal que no es finita y que tampoco es periódica, lo cual implica necesariamente que es un decimal cuyas cifras decimales son infinitas y ninguna porción de estas se repite, es decir, NO TIENE PERÍODO.
Ejemplos:
a) 4, 24681012141618...números pares
b) 1, 3571113171923293137...números primos
c) 1, 12345678910111213...números naturales
NÚMEROS QUE NO SE DEJAN ESCRIBIR COMO POTENCIA
{2,3,5,6,7,10,11,12,13,14,15,17,18,19,20,21,22,23,24,26,28,29,30,31,33,34,35,37,38,39,40,41,42,43,44,45,46,47,48,50,51,53}ñale la parte entera, la parte periódica y la parte no periódica:
TALLER.
SEÑALE LA PARTE ENTERA, LA PARTE PERIÓDICA Y LA PARTE NO PERIÓDICA:
1. 71,403405403403...
2. 102,102102102...
3. 603,989898...
4. 405,505050505...
5. 793,413413413...
6. 49,212121...
7. 503,015989898...
8. 68,213341341341...
9. 500,034415415415...
10. 71,6123939339...
11. 605,101101101...
12. 421,671151515...
Taller de repaso con números racionales.
SEMANA 8
MARZO 2 AL 6
1. Repaso de operaciones con racionales.
2. Repaso de ubicación de racionales en la recta numérica.
3. Repaso de conversión de racionales a decimales y ubicación en la recta numérica.
4. Clasificación de los decimales en periódicos puros, mixtos y exactos.
5. Conversión de periódico misto a racional y viceversa.
6. Conversión de periódico puro a racional y viceversa.
7. Taller de conversión de racionales a periódicos y su clasificación.
8. Evaluaciones de los puntos 1, 2 y 3. Queda pendiente para lunes 9 de marzo los puntos 4,5,6 y 7.
Los estudiantes deben aprenderse las tablas de multiplicar y repasar la división que están muy regulares en ello.
1. Repaso de operaciones con racionales.
2. Repaso de ubicación de racionales en la recta numérica.
3. Repaso de conversión de racionales a decimales y ubicación en la recta numérica.
4. Clasificación de los decimales en periódicos puros, mixtos y exactos.
5. Conversión de periódico misto a racional y viceversa.
6. Conversión de periódico puro a racional y viceversa.
7. Taller de conversión de racionales a periódicos y su clasificación.
8. Evaluaciones de los puntos 1, 2 y 3. Queda pendiente para lunes 9 de marzo los puntos 4,5,6 y 7.
Los estudiantes deben aprenderse las tablas de multiplicar y repasar la división que están muy regulares en ello.
domingo, 22 de febrero de 2015
SEMANA SIETE
FEBRERO 23 AL 27
LUNES 23
Terminar el taller nº 9 en clase.
Asignación del taller nº 10
Se evaluará en la segunda clase de la semana y deben llevar para comprar la fotocopia.
TALLER Nº 10
Operaciones con números racionales
LUNES 23
Terminar el taller nº 9 en clase.
Asignación del taller nº 10
Se evaluará en la segunda clase de la semana y deben llevar para comprar la fotocopia.
TALLER Nº 10
Operaciones con números racionales
Calcula las siguientes operaciones con números racionales
(haga todos los procedimientos):
(haga todos los procedimientos):
1 ![]()
2 ![]()
3 ![]()
4 ![]()
5.![]()
6.![]()
7. 

8. ![]()
9.![]()
10. 

Suscribirse a:
Entradas (Atom)








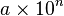


![\sqrt[3]{27\cdot 10^{12}} = 3\cdot 10^{4}](http://upload.wikimedia.org/math/a/f/d/afde53997fe13e5e0cceae4f2c01404a.png)
![\sqrt[4]{256\cdot 10^{64}} = 4\cdot 10^{16}](http://upload.wikimedia.org/math/5/e/1/5e1f77893e57922c5712801da277efcf.png)








