SEMANA 37

OCTUBRE 26 AL 30


Suma y diferencia de cubos-----Diferencia de cuadrados





Diferencia de cuadrados.

Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta y sus términos tienen distinto signo.

Al estudiar los productos notables teníamos que:

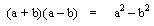
En donde el resultado es una diferencia de cuadrados, para este capítulo es el caso contrario:

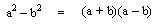
SE FACTORIZA: 

Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de las raíces.

Pasos:

1. Se extrae la raíz cuadrada de ambos términos.

2. Se multiplica la suma por la diferencia de estas cantidades (el segundo termino del binomio negativo es la raíz del termino del binomio que es negativo).

EJEMPLO 1: (Fácil) x2 - 9 = (x + 3).(x - 3) x     3 Los dos términos son cuadrados. Las "bases" son x y 3. Se factoriza multiplicando la "suma de las bases" por la "resta de las bases". EXPLICACIÓN DEL EJEMPLO 1  EJEMPLO 2: (Con dos letras) x2 - y2 = (x + y).(x - y) x     y Las dos bases son letras EXPLICACIÓN DEL EJEMPLO 2 EJEMPLO 3: (Con el "1") b2 - 1 = (b + 1).(b - 1) b     1 No hay que olvidar que el número 1 es un cuadrado. EXPLICACIÓN DEL EJEMPLO 3

EJEMPLO 4: (Con fracciones) x2 - 9/25 = (x + 3/5).(x - 3/5) x      3/5 9/25 es cuadrado. Porque 9 es cuadrado (de 3), y 25 también (de 5) EXPLICACIÓN DEL EJEMPLO 4 EJEMPLO 5: (Con potencias distintas de 2) x6 - 4 = (x3 + 2).(x3 - 2) x3   2 x6 es también un cuadrado, es el cuadrado de x3. Ya que (x3)2 es igual a x6 EXPLICACIÓN DEL EJEMPLO 5 EJEMPLO 6: (Con términos "compuestos") 36x2 - a6b4 = (6x + a3b2).(6x - a3b2)  6x       a3b2 Los términos pueden estar compuestos por varios factores, y no una sola letra o número. Pero todos deben ser cuadrados. EXPLICACIÓN DEL EJEMPLO 6 EJEMPLO 7: (Con números decimales) x2 - 0,16 = (x + 0,4).(x - 0,4) x     0,4 También se puede hacer pasando los números decimales a fracción (Ver en la EXPLICACIÓN) EXPLICACIÓN DEL EJEMPLO 7 EJEMPLO 8: (Con la resta "al revés") -x2 + 4 = 4 - x2 = (2 + x).(2 - x) x       2 El primer término es negativo y el segundo es positivo. Pero puedo escribirlos "al revés", y ahí tengo la resta que necesito. EXPLICACIÓN DEL EJEMPLO 8 EJEMPLO 9: (Uno "con todo") 4/25 x6a2 - 0,01 b4y10 = (2/5 x3a + 0,1 b2y5).(2/5 x3a - 0,1 b2y5) 2/5 x3a       0,1 b2y5 SUMA DE CUBOS Se identifica porque los dos términos tienen igual signo y a cada uno se le puede extraer raíz cúbica exacta. SE FACTORIZA: 1. Un binomio por un trinomio. 2. El binomio: Está formado por la suma de las raíces cúbicas de los términos. 3. El trinomio: Está formado por el cuadrado de la primera raíz, menos el producto de la primera por la segunda raíz, más el cuadrado de la segunda raíz. a3 + b3 = (a + b) · (a2 − ab + b2) 8x3 + 27 = (2x + 3) (4x2 - 6x + 9) DIFERENCA DE CUBOS SE FACTORIZA:  1. Un binomio por un trinomio. 2. El binomio: Formada por la diferencia de las raíces cúbicas de los términos. 3. El trinomio: es igual al cuadrado de la primera raíz,más el producto de las dos raíces, más el cuadrado de la segunda raíz. Ejemplos:  a3 – b3 = (a – b) (a2 + ab + b2)

SEMANA 36

OCTUBRE 19 A 23

Octubre 12 Festivo ( lunes)

En 8º a----lunes y jueves
Lunes (festivo)  y jueves (actividad por la semana de la convivencia)
1º hora: Actividad de integración lúdica en el patio cubierto.
2º hora:Actividad lúdica y de competencia, resaltando la necesidad de integración, la autonomía, la cooperación---en el aula de clase.

En 8º B-----miércoles y viernes

Miércoles:
Repaso de productos y cocientes notables, evaluación de cocientes notables.
Inicio del tema: Factor común.
Viernes: Continuación de factor común y taller de aplicación.

.

SEMANA 35

 OCTUBRE 12 AL 16

SEMANA DE LA CONVIVENCIA

Evaluación de cocientes notables en 8º a
Factorización y casos:
1. Factor común:

• Numérico
• Numérico literal.

¿Por qué se llama "Factor común"? 

Por que en general el Caso se aplica cuando en todos los términos hay un "factor común".


¿Pero qué es un "factor común"?

Es "algo" (número, letras, una "expresión algebraica") que está multiplicando en todos los términos. Tiene que estar en todos los términos, por eso es "común" (común a todos). Y recordemos además que, en una multiplicación, se les llama "factores" a los números que están multiplicándose. De ahí vienen las dos palabras: "factor" y "común".

Por ejemplo, en 2.a + 2.b + 2.c, está el factor común "2"; porque en todos los términos está multiplicando el número 2. En 5a + 7a + 4a, está el factor común "a"; porque en todos los términos está multiplicando la letra "a".

Pero no siempre es tan fácil identificar al factor común como en esos dos ejemplos, ya que en los términos puede haber números diferentes o letras con distinto exponente, y el factor común puede estar "oculto" entre ellos. En los ejercicios resueltos de esta misma página presento una variedad de situaciones en donde hay factor común, y explico cómo identificarlo. Y para más detalle se puede entrar en los enlaces de explicación de cada ejemplo.


¿Una vez que identifico al "factor común", qué hago para "sacarlo"?

Divido a todos los términos por ese factor. La división entre números ya la conocemos. La división entre letras iguales (potencias de igual base) se hace restando los exponentes. "Los números se dividen con los números", "las letras con las letras iguales". Por ejemplo:

4a - 8b + 6c =  

Allí el factor común es 2, entonces divido todos los términos por 2.

El resultado de esa división es:

2a - 4b + 3c

(Se aplica la Propiedad distributiva de la división respecto de la suma y la resta. Más detalle sobre el procedimiento en: EXPLICACIÓN DEL EJEMPLO 1)


¿Hay una regla para encontrar factor común entre los números, si no puedo descubrirlo intuitivamente?

Sí. Sobre todo cuando son números grandes, nos conviene saber que el factor común que nos piden sacar entre ellos es el conocido MÁXIMO COMÚN DIVISOR o DIVISOR COMÚN MAYOR (MCD o DCM). Es el mayor número por el cual podamos dividir a todos los términos.

¿Y cómo saco factor común entre las letras?

Y cuando una o más letras están en todos los términos, son factor común, y hay que sacarlas con el menor exponente con que aparecen (¿por qué?). Por ejemplo:7x² + 11x³ - 4x⁵ + 3x⁴  - x⁸ = 

En todos los términos está la "x". La "x" es factor común y hay que sacarla con exponente 2, porque es el menor exponente con el que aparece en el polinomio. El factor común común es: x².7x² + 11x³ - 4x⁵ + 3x⁴  - x⁸ = x². (7 + 11x - 4x³ + 3x² - x⁶)
Para dividir a las letras de los términos por las del factor común, hay que restar los exponentes, porque es división entre potencias de igual base (Propiedades de las potencias de igual base). Por ejemplo:

x⁵:x² = x^5-2 = x³

FACTOR COMÚN / EJERCICIOS RESUELTOS EJEMPLO 1: (Hay factor común entre los números) 8a - 4b + 16c + 12d = 4. (2a - b + 4c + 3d) El factor común es el número 4: El Máximo Común Divisor entre los números. EXPLICACIÓN DEL EJEMPLO 1  EJEMPLO 2: (Hay factor común entre las letras) 7x2 + 11x3 - 4x5 + 3x4  - x8 = x2. (7 + 11x - 4x3 + 3x2 - x6) El factor común es x2.: La x elevada a la menor potencia con que aparece. EXPLICACIÓN DEL EJEMPLO 2 EJEMPLO 3: (Hay factor común entre los números y entre las letras) 9x3 - 6x2 + 12x5 - 18x7 = 3x2. (3x - 2 + 4x3 - 6x5) El factor común es 3x2: El MCD entre los números y la x elevada a la menor potencia. EXPLICACIÓN DEL EJEMPLO 3 EJEMPLO 4: (Con fracciones) 4/3 x - 8/9 x3 + 16/15 x7 - 2/3 x5 = 2/3 x. (2 - 4/3 x2 + 8/5 x6 - x4) El factor común es 2/3 x: El MCD del numerador sobre el MCD del denominador, y la x a la menor potencia. EXPLICACIÓN DEL EJEMPLO 4

EJEMPLO 5: (Con varias letras diferentes) 9x2ab - 3xa2b3 + x2az = xa. (9xb - 3ab2 + xz) El factor común es xa. Las 2 letras que están en todos los términos, con la menor potencia con la que aparecen. EXPLICACIÓN DEL EJEMPLO 5 EJEMPLO 6: (Con números grandes) 36x4 - 48x6 - 72x3 + 60x5 = 12x3. (3x - 16x3 - 6 + 5x2)