ABRIL 27 A MAYO 1
PARO NACIONAL DE DUCADORES
lunes, 20 de abril de 2015
SEMANA 14
ABRIL 20 AL 24
ABRIL 22 INICIA PARO NACIONAL DE EDUCADORES.
NOTACIÓN CIENTÍFICA.
ABRIL 22 INICIA PARO NACIONAL DE EDUCADORES.
NOTACIÓN CIENTÍFICA.
La notación científica es una manera rápida de representar un número utilizando potencias de base diez. Esta notación se utiliza para poder expresar muy fácilmente números muy grandes o muy pequeños.
Los números se escriben como un producto:
siendo:
 un número real mayor o igual que 1 y menor que 10, que recibe el nombre de coeficiente.
un número real mayor o igual que 1 y menor que 10, que recibe el nombre de coeficiente. un número entero, que recibe el nombre de exponente u orden de magnitud.
un número entero, que recibe el nombre de exponente u orden de magnitud.
La notación científica utiliza un sistema llamado coma flotante, o de punto flotante en países de habla inglesa y en algunos hispanohablantes.
Historia
El primer intento de representar números demasiado grandes fue emprendido por el matemático y filósofo griego Arquímedes, descrito en su obra El contador de Arena en el siglo III a. C. Ideó un sistema de representación numérica para estimar cuántos granos de arena existían en el universo. El número estimado por él era de 1063 granos. Nótese la coincidencia del exponente con el número de casilleros del ajedrez sabiendo que para valores positivos, el exponente es n-1 donde n es el número de dígitos, siendo la última casilla la Nº 64 el exponente sería 63 (hay un antiguo cuento del tablero de ajedrez en que al último casillero le corresponde -2 elevado a la 63- granos).
A través de la notación científica fue concebido el modelo de representación de los números reales mediante coma flotante.
Escritura
- 100 = 1
- 101 = 10
- 102 = 100
- 103 = 1 000
- 104 = 10 000
- 105 = 100 000
- 106 = 1 000 000
- 107 = 10 000 000
- 108 = 100 000 000
- 109 = 1 000 000 000
- 1010 = 10 000 000 000
- 1020 = 100 000 000 000 000 000 000
- 1030 = 1 000 000 000 000 000 000 000 000 000 000
10 elevado a una potencia entera negativa –n es igual a 1/10n:
- 10–1 = 1/10 = 0,1
- 10–2 = 1/100 = 0,01
- 10–3 = 1/1 000 = 0,001
- 10–9 = 1/1 000 000 000 = 0,000 000 001
- 10-12 = 1/1 000 000 000 000 = 0,000 000 000 001
- 10-15 = 1/1 000 000 000 000 000 = 0,000 000 000 000 001
- 10-17 = 1/ 1 000 000 000 000 000 00 = 0,000 000 000 000 000 01
Por tanto, un número como: 156 234 000 000 000 000 000 000 000 000 debe ser escrito como 1,56234×1029,
y un número pequeño como 0,000 000 000 000 000 000 000 000 000 000 910 939 kg (masa de un electrón) debe ser escrito como 9,10939×10–31kg.
Operaciones matemáticas con notación científica
Suma y resta
Siempre que las potencias de 10 sean las mismas, se deben sumar los coeficientes, dejando la potencia de 10 con el mismo grado. En caso de que no tengan el mismo exponente, debe convertirse el coeficiente, multiplicándolo o dividiéndolo por 10 tantas veces como se necesite para obtener el mismo exponente.
Ejemplos:
- 2×105 + 3×105 = 5×105
- 3×105 - 0.2×105 = 2.8×105
- 2×104 + 3 ×105 - 6 ×103 = (tomamos el exponente 5 como referencia)
- = 0,2 × 105 + 3 × 105 - 0,06 ×105 = 3,14 ×105
Multiplicación
Para multiplicar cantidades escritas en notación científica se multiplican los coeficientes y se suman los exponentes.
Ejemplo:
- (4×1012)×(2×105) =8×1017
División
Para dividir cantidades escritas en notación científica se dividen los coeficientes y se restan los exponentes.
Ejemplo: 

 .
.


 .
.Potenciación
Se eleva el coeficiente a la potencia y se multiplican los exponentes.
Ejemplo: (3×106)2 = 9 ×1012.
Radicación
Se debe extraer la raíz del coeficiente y se divide el exponente entre el índice de la raíz.
Ejemplos:
domingo, 12 de abril de 2015
SEMANA DOCE
ABRIL 6 AL 10
ABRIL 6---CALAMIDAD DOMÉSTICA---NO DICTÉ CLASES
ABRIL 7 AL 10
Historia de los números irracionales
ABRIL 6---CALAMIDAD DOMÉSTICA---NO DICTÉ CLASES
ABRIL 7 AL 10
Historia de los números irracionales
Aparentemente Hipaso (un estudiante de Pitágoras) descubrió los números irracionales intentando escribir la raíz de 2 en forma de fracción (se cree que usando geometría). Pero en su lugar demostró que no se puede escribir como fracción, así que es irracional.
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!
SEMANA 11
MARZO 23 A 27
MARZO 23-----FESTIVO
CALAMIDAD DOMÉSTICA (NO DICTÉ CLASES TODA LA SEMANA)
MARZO 30 A ABRIL 3----SEMANA SANTA
MARZO 23-----FESTIVO
CALAMIDAD DOMÉSTICA (NO DICTÉ CLASES TODA LA SEMANA)
MARZO 30 A ABRIL 3----SEMANA SANTA
domingo, 15 de marzo de 2015
SEMANA DIEZ
MARZO 16 A 20
IDENTIFICACIÓN DE LOS NÚMEROS IRRACIONALES ( I )
Los números que no se pueden representar por un racional se llaman irracionales. Hay números decimales , cuyas fracciones son periódicas, es decir que se repiten a partir de cierto número. Ejem:
7/3 = 2,333... 32/25= 1,282828... 781/250= 3,124124124...
Son fracciones periódicas y éstas se pueden representar por un racional.
Pero existen otros números cuyos decimales son infinitos, sin repetir períodos y que no pueden escribirse como racionales, esos números son los llamados Irracionales.
Ejm:
Lo mismo ocurre con la raíz cuadrada de dos: 1, 4142136...que se aproxima a 1,4142 aunque no tenga límite.
La raíz de cualquier número natural que no se deja escribir como una potencia. Ejemplos:
a los racionales y "I" los irracionales.
Si unimos los racionales "Q" con los irracionales "I" se forman los reales "R"
Los números irracionales se pueden representar en la RECTA NUMÉRICA.
A cada número racional le corresponde un punto en la recta pero en realidad éstos no completan la recta, también la constituyen los irracionales. En general, representar un número con infinitas cifras decimales no periódicas es imposible y por lo tanto nos tendríamos que conformar con una aproximación. De todas maneras, hay métodos geométricos que permiten representar algunos números irracionales en la recta numérica.
Veamos como se puede representar, por ejemplo, :
hay que tener claro que =1,414...,es decir, 1<
=1,414...,es decir, 1<  < 2
< 2
Observa el cuadrado del dibujo, si ampliamos el teorema de Pitágoras para hallar su diagonal comprendemos esto
Con la ayuda de un compás podemos representar exactamente en la recta numérica.
en la recta numérica.
Sabemos que es un número irracional, por lo tanto,
es un número irracional, por lo tanto,
Historia de los números irracionales
Aparentemente Hipaso (un estudiante de Pitágoras) descubrió los números irracionales intentando escribir la raíz de 2 en forma de fracción (se cree que usando geometría). Pero en su lugar demostró que no se puede escribir como fracción, así que es irracional.
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!
IDENTIFICACIÓN DE LOS NÚMEROS IRRACIONALES ( I )
Los números que no se pueden representar por un racional se llaman irracionales. Hay números decimales , cuyas fracciones son periódicas, es decir que se repiten a partir de cierto número. Ejem:
7/3 = 2,333... 32/25= 1,282828... 781/250= 3,124124124...
Son fracciones periódicas y éstas se pueden representar por un racional.
Pero existen otros números cuyos decimales son infinitos, sin repetir períodos y que no pueden escribirse como racionales, esos números son los llamados Irracionales.
Ejm:
3, 1415275926535897932384626433832795 (y más...) ... que es conocido como pi.
que se aproxima a 3,1416 y que sale de dividir la longitud de la circunferencia entre el diámetro.Lo mismo ocurre con la raíz cuadrada de dos: 1, 4142136...que se aproxima a 1,4142 aunque no tenga límite.
La raíz de cualquier número natural que no se deja escribir como una potencia. Ejemplos:
a los racionales y "I" los irracionales.
Si unimos los racionales "Q" con los irracionales "I" se forman los reales "R"
Los números irracionales se pueden representar en la RECTA NUMÉRICA.
A cada número racional le corresponde un punto en la recta pero en realidad éstos no completan la recta, también la constituyen los irracionales. En general, representar un número con infinitas cifras decimales no periódicas es imposible y por lo tanto nos tendríamos que conformar con una aproximación. De todas maneras, hay métodos geométricos que permiten representar algunos números irracionales en la recta numérica.
Veamos como se puede representar, por ejemplo, :

hay que tener claro que
 =1,414...,es decir, 1<
=1,414...,es decir, 1<  < 2
< 2Observa el cuadrado del dibujo, si ampliamos el teorema de Pitágoras para hallar su diagonal comprendemos esto
Con la ayuda de un compás podemos representar exactamente
 en la recta numérica.
en la recta numérica.Sabemos que
 es un número irracional, por lo tanto,
es un número irracional, por lo tanto,
el punto P de la recta no puede estar ocupado por ningún otro número irracional.
Números irracionales famosos
domingo, 8 de marzo de 2015
SEMANA NUEVE
MARZO 9 AL 13
NÚMEROS IRRACIONALES.
Un número irracional es aquél cuya representación decimal no se puede expresar como el cociente de dos números enteros, es decir como un número racional.
esto significa que un número irracional es una expresión decimal que no es finita y que tampoco es periódica, lo cual implica necesariamente que es un decimal cuyas cifras decimales son infinitas y ninguna porción de estas se repite, es decir, NO TIENE PERÍODO.
Ejemplos:
a) 4, 24681012141618...números pares
b) 1, 3571113171923293137...números primos
c) 1, 12345678910111213...números naturales
NÚMEROS QUE NO SE DEJAN ESCRIBIR COMO POTENCIA
{2,3,5,6,7,10,11,12,13,14,15,17,18,19,20,21,22,23,24,26,28,29,30,31,33,34,35,37,38,39,40,41,42,43,44,45,46,47,48,50,51,53}ñale la parte entera, la parte periódica y la parte no periódica:
TALLER.
SEÑALE LA PARTE ENTERA, LA PARTE PERIÓDICA Y LA PARTE NO PERIÓDICA:
1. 71,403405403403...
2. 102,102102102...
3. 603,989898...
4. 405,505050505...
5. 793,413413413...
6. 49,212121...
7. 503,015989898...
8. 68,213341341341...
9. 500,034415415415...
10. 71,6123939339...
11. 605,101101101...
12. 421,671151515...
Taller de repaso con números racionales.
NÚMEROS IRRACIONALES.
Un número irracional es aquél cuya representación decimal no se puede expresar como el cociente de dos números enteros, es decir como un número racional.
esto significa que un número irracional es una expresión decimal que no es finita y que tampoco es periódica, lo cual implica necesariamente que es un decimal cuyas cifras decimales son infinitas y ninguna porción de estas se repite, es decir, NO TIENE PERÍODO.
Ejemplos:
a) 4, 24681012141618...números pares
b) 1, 3571113171923293137...números primos
c) 1, 12345678910111213...números naturales
NÚMEROS QUE NO SE DEJAN ESCRIBIR COMO POTENCIA
{2,3,5,6,7,10,11,12,13,14,15,17,18,19,20,21,22,23,24,26,28,29,30,31,33,34,35,37,38,39,40,41,42,43,44,45,46,47,48,50,51,53}ñale la parte entera, la parte periódica y la parte no periódica:
TALLER.
SEÑALE LA PARTE ENTERA, LA PARTE PERIÓDICA Y LA PARTE NO PERIÓDICA:
1. 71,403405403403...
2. 102,102102102...
3. 603,989898...
4. 405,505050505...
5. 793,413413413...
6. 49,212121...
7. 503,015989898...
8. 68,213341341341...
9. 500,034415415415...
10. 71,6123939339...
11. 605,101101101...
12. 421,671151515...
Taller de repaso con números racionales.
SEMANA 8
MARZO 2 AL 6
1. Repaso de operaciones con racionales.
2. Repaso de ubicación de racionales en la recta numérica.
3. Repaso de conversión de racionales a decimales y ubicación en la recta numérica.
4. Clasificación de los decimales en periódicos puros, mixtos y exactos.
5. Conversión de periódico misto a racional y viceversa.
6. Conversión de periódico puro a racional y viceversa.
7. Taller de conversión de racionales a periódicos y su clasificación.
8. Evaluaciones de los puntos 1, 2 y 3. Queda pendiente para lunes 9 de marzo los puntos 4,5,6 y 7.
Los estudiantes deben aprenderse las tablas de multiplicar y repasar la división que están muy regulares en ello.
1. Repaso de operaciones con racionales.
2. Repaso de ubicación de racionales en la recta numérica.
3. Repaso de conversión de racionales a decimales y ubicación en la recta numérica.
4. Clasificación de los decimales en periódicos puros, mixtos y exactos.
5. Conversión de periódico misto a racional y viceversa.
6. Conversión de periódico puro a racional y viceversa.
7. Taller de conversión de racionales a periódicos y su clasificación.
8. Evaluaciones de los puntos 1, 2 y 3. Queda pendiente para lunes 9 de marzo los puntos 4,5,6 y 7.
Los estudiantes deben aprenderse las tablas de multiplicar y repasar la división que están muy regulares en ello.
domingo, 22 de febrero de 2015
SEMANA SIETE
FEBRERO 23 AL 27
LUNES 23
Terminar el taller nº 9 en clase.
Asignación del taller nº 10
Se evaluará en la segunda clase de la semana y deben llevar para comprar la fotocopia.
TALLER Nº 10
Operaciones con números racionales
LUNES 23
Terminar el taller nº 9 en clase.
Asignación del taller nº 10
Se evaluará en la segunda clase de la semana y deben llevar para comprar la fotocopia.
TALLER Nº 10
Operaciones con números racionales
Calcula las siguientes operaciones con números racionales
(haga todos los procedimientos):
(haga todos los procedimientos):
1 ![]()
2 ![]()
3 ![]()
4 ![]()
5.![]()
6.![]()
7. 

8. ![]()
9.![]()
10. 

domingo, 15 de febrero de 2015
SEMANA SEIS
FEBRERO 16 AL 20
8A Y 8B
Evaluación escrita de suma, resta, multiplicación y división de enteros, polinomios.( Lunes para octavo B y miércoles para octavo A.
Llevar calculadora para la segunda clase de la semana.
REPRESENTACIÓN DECIMAL DE LOS NÚMEROS RACIONALES.
Todo número racional se puede expresar como número decimal.
Para lograrlo, se efectúa la operación de división del numerador entre el denominador. Después de hacerlo puede resultar que se obtenga como resultado:
1. Una expresión decimal exacta.
2. Una expresión decimal periódica pura.
3. Una expresión decimal periódica mixta.
- Expresión decimal exacta: Si tiene un número finito de cifras decimales.
- Por ejemplo:
- a)
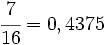
- b) 7, 0356 P.E ( parte entera) = 7
- C.F. ( cantidad de factores) = 4 --------es un decimal exacto o finito.
- c) 1253,0 P.E = 1253
- C.F.=1 ------es un decimal exacto o finito.
- EJEMPLOS:
- Convertir los siguientes racionales a decimales exactos o finitos:
- a) 307/ 125 = 2, 456 P.E =2 C.F= 3
- b) 2576 / 100 = 25,76 P.E= 25 C.F= 2
- c) 2397 / 32 = 74,90625 P.E= 74 C.F= 5
- NOTA: Cuando el dividendo es más pequeño que el divisor, se le agregan tantos ceros al dividendo para que quede mayor que el divisor.
- Se efectúa la división normalmente y luego el resultado se divide por la potencia de diez que tiene tantos ceros como los agregados al divisor. Ejms:
- A) 3 / 250 entonces al 3 le agregamos dos ceros y dividimos normalmente. Así queda:
- 300 / 250 = 1,2 P.E= 1 C.F= 1
- B) 1,2 / 100 = 0,012 P.E= 0 C.F= 3
- C) 9/16 = 0,5625 P.E= 0 C.F= 4
- EXPRESIONES DECIMALES EXACTAS A NÚMERO RACIONAL
Para convertir un número decimal exacto a fracción, escribimos el mismo número sin la coma en el numerador, y, como denominador escribimos el número uno, seguido de tantos ceros como cifras decimales tenga el número dado. Ejemplos:
Observe el video.- Ejemplos:
- Convertir los siguientes números decimales ( exactos) a racionales:
- a) 2,0356= 20356/ 10000= 10178/ 5000= 5089/2500
- b) 0, 0075= 75/ 10000 = 15/2000= 3/400
- c) 0,156= 156/1000= 78/500=39/250
- Expresión decimal periódica pura: Son números decimales que tienen después de la coma decimal uno o varios números que se repiten en forma sucesiva. El número o números que se repiten después de la coma decimal, se llama periodo.
- Por ejemplo:
-
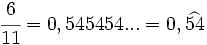 . El periodo es 54.
. El periodo es 54. - Expresión decimal periódica mixta: Si tiene un número infinito de decimales que se repiten a partir de una cierta posición decimal. La parte que se repite se llama periodo y la parte decimal previa al periodo se llama anteperíodo.
- Por ejemplo:
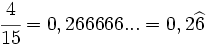 . El periodo es 6 y el anteperiodo 2.
. El periodo es 6 y el anteperiodo 2.
Se puede saber, sin hacer la división, que tipo de expresión decimal tiene una fracción. Para ello, deberemos simplificar la fracción y nos fijaremos en la descomposición del denominador en factores primos. Tendremos los siguientes casos:
Identificar el tipo de expresión decimal sin hacer la división
- Si el denominador sólo contiene factores que sean 2 ó 5, la fracción tiene una expresión decimal exacta.
Que diferencias hay entre la expresión
decimal periódica pura y la expresión
decimal perdiódica mixta?
decimal periódica pura y la expresión
decimal perdiódica mixta?
Una expresión decimal periódica pura es aquella cuyas cifras decimales
son todas periódicas 0,33333.......
1,23232323.....
3,345345345....
Para transformar una expresión decimal periódica pura Se pone en el
numerador el número sin coma y se le resta la parte no periódica;
en el denominador tantos nueves como cifras periódicas tenga
0,77777.... = 7/9
2,8888...... = (28-2) /9 = 26/9
1,595959... = (159-1)/99 = 158/99
3,497497497... = (1497-3)/999 = 1494/999
Una expresión decimal periódica mixta es aquella cuyas cifras decimales
son algunas periódicas y otras no. Así:
0,67777777.....
3,7845454545....
2,30963963963.....
Para transformar una expresion decimal mixta se pone en el numerador
el número entero sin coma
Se le resta la parte no periódica;
En el denominador tantos nueves como cifras periódicas tenga y tantos
ceros como cifras no periódicas. Así:
0,57777.. = (57 - 5) /90 = 52/90
0,4676767... = (467- 4) / 990 = 463 /990
0,95737373... = (9573 - 95) / 9900 = 9878 / 9900
5, 07383838... = (50738 - 507) / 9900 = 50231 / 9900
son todas periódicas 0,33333.......
1,23232323.....
3,345345345....
Para transformar una expresión decimal periódica pura Se pone en el
numerador el número sin coma y se le resta la parte no periódica;
en el denominador tantos nueves como cifras periódicas tenga
0,77777.... = 7/9
2,8888...... = (28-2) /9 = 26/9
1,595959... = (159-1)/99 = 158/99
3,497497497... = (1497-3)/999 = 1494/999
Una expresión decimal periódica mixta es aquella cuyas cifras decimales
son algunas periódicas y otras no. Así:
0,67777777.....
3,7845454545....
2,30963963963.....
Para transformar una expresion decimal mixta se pone en el numerador
el número entero sin coma
Se le resta la parte no periódica;
En el denominador tantos nueves como cifras periódicas tenga y tantos
ceros como cifras no periódicas. Así:
0,57777.. = (57 - 5) /90 = 52/90
0,4676767... = (467- 4) / 990 = 463 /990
0,95737373... = (9573 - 95) / 9900 = 9878 / 9900
5, 07383838... = (50738 - 507) / 9900 = 50231 / 9900
TALLER Nº 9
domingo, 8 de febrero de 2015
SEMANA cinco
FEBRERO 9 AL 13
TALLER Nº 8
Efectúe las siguiente operaciones con racionales:
TALLER Nº 8
Efectúe las siguiente operaciones con racionales:
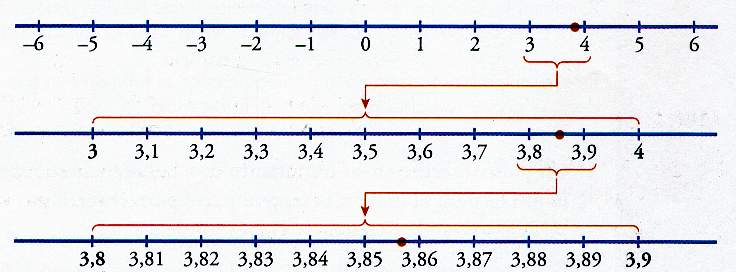
Representación de números decimales
Los números decimales los podemos representar en la recta real de la siguiente manera:
El punto rojo representa el número 3,85...
domingo, 1 de febrero de 2015
SEMANA CUATRO.
FEBRERO 2 AL 6
Lunes 8B
Miércoles 8A
Jueves 8A y 8B
NÚMEROS RACIONALES "Q"
 Número racional es todo número que puede representarse como el cociente de dos números enteros, más precisamente, un entero y un natural positivo, es decir, una fracción común
Número racional es todo número que puede representarse como el cociente de dos números enteros, más precisamente, un entero y un natural positivo, es decir, una fracción común  ; donde a se llama numerador y b se llama denominador, pero b es distinto de cero.
; donde a se llama numerador y b se llama denominador, pero b es distinto de cero.
El conjunto de los números racionales se denota por "Q ".
La escritura decimal de un número racional es, o bien un número decimal finito, o bien periódico.
En sentido estricto, número racional es el conjunto de todas las fracciones equivalentes a una dada.

PROPIEDADES DE LOS NÚMEROS RACIONALES.
1. El conjunto de los números racionales tienen infinita cantidad de elementos.
2. No tiene un primer ni un último elemento.
3. Entre dos números racionales, existe cantidad infinita de números racionales.
4. Ningún número racional tiene sucesor, ni antecesor.
5. Los números racionales no completan la recta numérica.
6. A todo número racional se le puede hacer corresponder un punto de la recta, pero no necesariamente todo punto de la recta corresponde a un número racional.
7. Se cumple que
REPRESENTACIÓN GRÁFICA DE NÚMEROS RACIONALES.
El conjunto de números racionales "Q", se pueden representar en la recta numérica de tal manera que la recta se vaya haciendo más completa.
Si se divide en dos partes iguales cada segmento unidad en la recta numérica, podemos representar los números racionales cuya representación fraccionaria tiene como denominador 2, como se muestra en el ejemplo siguiente:
Si se dividen en tres partes iguales cada segmento unidad en la recta, podemos representar los números racionales cuya representación fraccionaria tiene como denominador 3, como se muestra en el ejemplo siguiente:
Miércoles 8A
Jueves 8A y 8B
NÚMEROS RACIONALES "Q"
 Número racional es todo número que puede representarse como el cociente de dos números enteros, más precisamente, un entero y un natural positivo, es decir, una fracción común
Número racional es todo número que puede representarse como el cociente de dos números enteros, más precisamente, un entero y un natural positivo, es decir, una fracción común  ; donde a se llama numerador y b se llama denominador, pero b es distinto de cero.
; donde a se llama numerador y b se llama denominador, pero b es distinto de cero. El conjunto de los números racionales se denota por "Q ".
La escritura decimal de un número racional es, o bien un número decimal finito, o bien periódico.
En sentido estricto, número racional es el conjunto de todas las fracciones equivalentes a una dada.

PROPIEDADES DE LOS NÚMEROS RACIONALES.
1. El conjunto de los números racionales tienen infinita cantidad de elementos.
2. No tiene un primer ni un último elemento.
3. Entre dos números racionales, existe cantidad infinita de números racionales.
4. Ningún número racional tiene sucesor, ni antecesor.
5. Los números racionales no completan la recta numérica.
6. A todo número racional se le puede hacer corresponder un punto de la recta, pero no necesariamente todo punto de la recta corresponde a un número racional.
7. Se cumple que
Opuesto de un número racional | |
Para cada número racional
Dada la última observación se deduce que un número racional y su opuesto tienen "signo contrario". Por ejemplo:
|
El conjunto de números racionales "Q", se pueden representar en la recta numérica de tal manera que la recta se vaya haciendo más completa.
Si se divide en dos partes iguales cada segmento unidad en la recta numérica, podemos representar los números racionales cuya representación fraccionaria tiene como denominador 2, como se muestra en el ejemplo siguiente:
| Ejemplo Represente en la recta numérica los siguientes números racionales: |
Si se dividen en tres partes iguales cada segmento unidad en la recta, podemos representar los números racionales cuya representación fraccionaria tiene como denominador 3, como se muestra en el ejemplo siguiente:
| Ejemplo Represente en la recta numérica los siguientes números racionales: |
De igual manera, si se dividen en tres partes iguales cada segmento unidad en la recta, podemos representar los números racionales cuya representación fraccionaria tiene como denominador 3, como se muestra en el ejemplo siguiente:
| Ejemplo Represente en la recta numérica los siguientes números racionales: |
Generalizando el procedimiento descrito anteriormente se puede representar cualquier número racional en la recta numérica.
Nota: También se pueden representar los números racionales en la recta numérica, considerando su expansión decimal y ubicándolos en forma aproximada en la recta numérica, como se muestra en el ejemplo siguiente.
| Ejemplo Represente en una recta numérica los siguientes números racionales. Utilizando la calculadora se puede notar que: |

El número racional  y su opuesto
y su opuesto  se representan en la recta numérica a la misma distancia de cero, en sentidos opuestos.
se representan en la recta numérica a la misma distancia de cero, en sentidos opuestos.

Como conclusión, un número racional y su opuesto tienen "signo contrario".
|
3. Represente en una recta numérica los siguientes números racionales:
4. Para cada uno de los siguientes números racionales, determine su opuesto y represente ambos números en la recta numérica:
En estos dos últimos puntos del cuarto, simplemente es encontrar el opuesto de

 y localizarlos en la recta numérica. Nótese que son tres unidades con 3 décimas en uno y 8 unidades con 3 décimas en otro.
y localizarlos en la recta numérica. Nótese que son tres unidades con 3 décimas en uno y 8 unidades con 3 décimas en otro.
TALLER Nº 7
Suscribirse a:
Entradas (Atom)
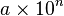


![\sqrt[3]{27\cdot 10^{12}} = 3\cdot 10^{4}](http://upload.wikimedia.org/math/a/f/d/afde53997fe13e5e0cceae4f2c01404a.png)
![\sqrt[4]{256\cdot 10^{64}} = 4\cdot 10^{16}](http://upload.wikimedia.org/math/5/e/1/5e1f77893e57922c5712801da277efcf.png)













.jpg)
